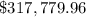Answer:
Part a) The lake frontage of lot A is
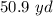
Part b) The lake frontage of lot B is

Part c) The lake frontage of lot C is

Part d) The prices of the other lots, from least to greatest, are
 and
and
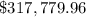
Explanation:
we know that
If two figures are similar, then the ratios of its corresponding sides is equal
Find the lake frontage (to the nearest tenth) of each lot shown
we have that
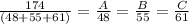

step 1
Find the lake frontage of lot A
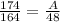
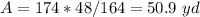
step 2
Find the lake frontage of lot B
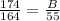

step 3
Find the lake frontage of lot C
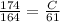
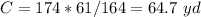
step 4
Find the prices of the other lots
we know that the price of the lot A is
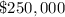 (given problem)
(given problem)
so
by proportion
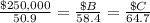
Find the price lot B

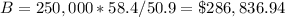
Find the price lot C
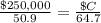
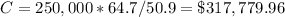
The prices of the other lots, from least to greatest, are
 and
and