Question

PLEASE HELPPPPPPP!!!!! I NEED MATH HELP QUICK!!!

1.) Choose the two points you would use to find the slope of the secant line for the function y = 2x^2 + 3x.
(x1, y1); (x2, y2)
(x, 2x^2 + 3x); (y, 2y^2 + 3y)
(x, 2x^2 + 3x); (x + Δx, 2(x + Δx)^2 + 3(x + Δx))
(x, x + Δx); (x + Δx, 2(x + Δx)^2 + 3(x + Δx))

2.) What is the slope of the secant line to the function given in question 1?
4x + 3
4x + 2Δx + 3
4x
2Δx + 3

3.) Find the formula for the slope of the line tangent to the curve given in question 1. 3
3x + 4
2x + 3
4x + 3

4.) Find the equation of the line tangent to the curve given in question 1, at the point (-2, 2).
y - 2 = -5(x + 2)
y + 2 = -5(x - 2)
y - 2 = 5(x - 2)
y + 2 = -5(x + 2)

You can answer any one of these! Please help!!!

Answer 1

1. Answer:

(x, 2x^2 + 3x); (x + Δx, 2(x + Δx)^2 + 3(x + Δx))

A secant of a curve is a line intersecting the curve in at least two different points. On the other hand, the slope of a secant line is the difference between the y values of these points divided by the difference between the x values. The secant to curve
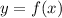`y= f(x)` is determined by the points
`(x, f(x))` and
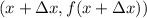`(x+\Delta x, f(x+ \Delta x))` so according to this definition the correct option is:

`\boxed{(x, 2x^2 + 3x); (x + \Delta x, 2(x + \Delta x)^2 + 3(x + \Delta x))}`

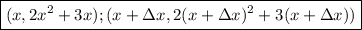
2. Answer:

4x + 2Δx + 3

As we said above, the slope of a secant line is the difference between the y values of these points divided by the difference between the x values. Therefore:

`m_(sec)=(2(x + \Delta x)^2 + 3(x + \Delta x)-(2x^2 + 3x))/(x + \Delta x-x) \\ \\ Applying \ square \ of \ the \ sum \ in \ the \ numerator: \\ \\m_(sec)=(2(x^2+2x\Delta x + \Delta x^2) + 3x + 3\Delta x-2x^2-3x)/(\Delta x) \\ \\m_(sec)=(2x^2+4x\Delta x + 2\Delta x^2+3x+3\Delta x-2x^2-3x)/(\Delta x) \\ \\m_(sec)=(4x\Delta x + 2\Delta x^2+3\Delta x)/(\Delta x)`

`Common \ factor \ \Delta x\\ \\m_(sec)=(\Delta x(4x+2\Delta x+3))/(\Delta x) \\ \\ Solving: \\ \\ \boxed{m_(sec)=4x+2\Delta x+3}`

3. Answer:

4x + 3

We have found the slope of the secant line and is:

`m_(sec)=4x+2\Delta x+3`

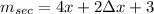
So a value of Δx close to zero gives us an amazing approximation to the slope of the tangent line we are looking for. Therefore, to find the slope of this tangent line we have:

Δx ≈ 0

Thus:

`m_(tan)=4x+2(0)+3 \\ \\ \therefore \boxed{m_(tan)=4x+3}`

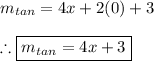
4. Answer:

y - 2 = -5(x + 2)

We have know the equation of the slope of the tangent line which is:

`m_(tan)=4x+3`

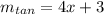
Therefore, at the point (-2, 2) the slope of the tangent line is:

`m=4(-2)+3 \\ \\ \therefore m=-5`

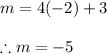
A line can be found by the equation:

`y-y_(0)=m(x-x_(0)) \\ \\ Where \ (x_(0), y_(0)) \ is \ a \ point \ of \ the \ line \\ \\ and \ (x_(0), y_(0))=(-2, 2)`

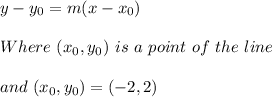
Thus:

`y-2=-5[x-(-2)] \\ \\ \therefore \boxed{y-2=-5(x+2)}`