Question

The graph below have the same shape . What is the equation of the red graph ?

A. G(x) = (7-x)^2
B. G(x) = 1-x^2
C. G(x) = 7-x^2
D. G(x) = (1-x)^2

Answer 1

Option B is correct .

Explanation:

According to Question , both the graph have same shape . If we look at the the first graph it cuts x - axis at (0 , 2) and ( 0 , -2) . Hence x = 2 and -2 are the zeroes of the equation .

And ,the given function is ,

`\implies f(x) = 4 - x^2 \\\\\implies f(x) = 4-x^2=0 \\\\\implies 2^2-x^2=0\\\\\implies (2-x)(2+x) = 0 \\\\\boxed{\red{\bf \implies x = 2 , (-2) }}`

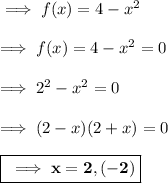
• Hence ,we can can see that x = 2 and (-2) are the zeroes of graph.

This implies that if we know the zeroes , we can frame the Equation.

On looking at second parabola , it's clear that cuts x - axis at ( 1, 0 ) and (-1,0). So , 1 and -1 are the zeroes of the quadratic equation . Let the function be g(x) . Here , a and ß are the zeroes.

`\begin{lgathered}\implies g(x) = (x-\alpha)(x-\beta) \\\\\implies g(x) = (1+x)(1-x) \\\\\boxed{\pink{\bf \implies g(x) = 1 - x^2}}\end{lgathered}`

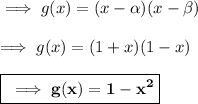
Hence option B is correct .