Question

I need help on HOW to solve these types of questions. Not the answer. The section is on Exponential Equations. It has to do something with a(b)^x

This is confusing because on number 12 it is not same format for number 14. Idk it looks weird because there is parentheses around a lot of numbers. Please see the attached file.

Answer 1

11. Divide both sides by 2:

`2\left(\frac19\right)^x=\frac2{81}\implies\left(\frac19\right)^x=\frac1{81}`

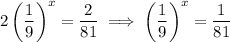
The solution has to be
`x=2` because

`\left(\frac19\right)^2=(1^2)/(9^2)=\frac1{81}`

12. Divide both sides by 2:

`2\left(\frac4{13}\right)^x=(32)/(169)\implies\left(\frac4{13}\right)^x=(16)/(169)`

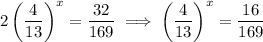
On the right side we have two perfect squares:

`\left(\frac4{13}\right)^x=(4^2)/(13^2)=\left(\frac4{13}\right)^2`

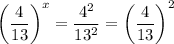
so again the answer is
`x=2`.

14. Divide both sides by 8:

`8\left(\frac23\right)^x=4\left((16)/(27)\right)\implies\left(\frac23\right)^x=\frac8{27}`

On the right we have perfect cubes:

`\left(\frac23\right)^x=(2^3)/(3^3)=\left(\frac23\right)^3`

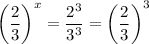
so
`x=3`.

15.
`\frac25\left(\frac25\right)^x=\frac8{125}`

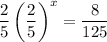
We could divide both sides by 2/5 (or multiply both sides by 5/2, as the writing on your paper suggests). Then

`\left(\frac25\right)^x=(40)/(250)=\frac4{25}`

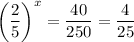
The right side has two perfect squares:

`\left(\frac25\right)^x=(2^2)/(5^2)=\left(\frac25\right)^2`

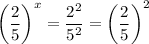
so that
`x=2`.

Another way to do this is to rewrite the left side as

`\frac25\left(\frac25\right)^x=\left(\frac25\right)^1\left(\frac25\right)^x=\left(\frac25\right)^(x+1)`

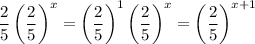
Meanwhile, on the right we have two perfect cubes:

`\left(\frac25\right)^(x+1)=(2^3)/(5^3)=\left(\frac25\right)^3`

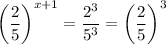
so that
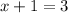`x+1=3`, or
`x=2`, as before.