Question

Can you please show the work on both of them? ​

Answer 1

Question 9)

From the line graph, taking two points

• (-5, 4)

• (-6, 7)

Finding the slope between (-5, 4) and (-6, 7)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(-5,\:4\right),\:\left(x_2,\:y_2\right)=\left(-6,\:7\right)`

`m=(7-4)/(-6-\left(-5\right))`

`m=-3`

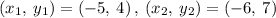
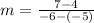
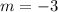
We know that the slope-intercept of the line equation is

y = mx+b

where m is the slope and b is the y-intercept

substituting (-5, 4) and m = -3 in the slope-intercept of the line

y = mx+b

4 = -3(-5)+b

4 = 15+b

b = 4-15

b = -11

substituting b = -10 and m = -3 in the slope-intercept of the line

y = mx+b

y = -3x+(-11)

y = -3x - 11

Thus, equation is slope-intercept form will be:

y = -3x - 11

Hence, option B is true.

Question 10)

From the line graph, taking two points

• (4, 7)

• (-8, 1)

Finding the slope between (4, 7) and (-8, 1)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(4,\:7\right),\:\left(x_2,\:y_2\right)=\left(-8,\:1\right)`

`m=(1-7)/(-8-4)`

`m=(1)/(2)`

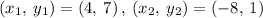
We know that the slope-intercept of the line equation is

y = mx+b

where m is the slope and b is the y-intercept

substituting (4, 7) and m = 1/2 in the slope-intercept of the line

y = mx+b

7 = 1/2(4)+b

7 = 2+b

b = 5

substituting b = 5 and m = 1/2 in the slope-intercept of the line

y = mx+b

y = 1/2x + 5

Thus, the equation is slope-intercept form will be:

y = 1/2x + 5

Hence, option C is true.