Question

Give the solutions from this questions. 50 Pointss

Answer 1

the pdf wont load

Explanation:

Answer 2

7. Answer: P(x) =
`\bold{(3)/(4)}`(x³ 1 x² - 10x + 6)

Explanation:

The factored form of a polynomial is: a(x - p)(x-q)...(x-z) . where p, q, ..., z are the roots.

Convert the roots into factors, include conjugates of any complex roots, and multiply all of the factors. Then find the a-value.

roots: x = 3 x = 2 + √2 x = 2 - √2 (conjugate)

factors: x - 3 = 0 x - 2 - √2 = 0 x - 2 + √2 = 0

(x - 3)(x - 2 - √2)(x - 2 + √2)

multiply the complex roots:

(x + 3)(x² - 4x + 2)

distribute (x + 3) to find the basic polynomial

x³ + x² - 10x + 6

Next, find the a-value:

P(x) = a(x³ + x² - 10x + 6)

P(1) = a(1 - 1 - 10 + 6) = -3

-4a = -3

`a=(3)/(4)`

`\boxed{P(x)=(3)/(4)(x^3-x^2-10x+6)}`

***********************************************************************************

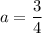
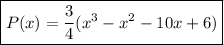
8. Answer: P(x) =
`\bold{(1)/(2)}`(x⁴ + 8)

Explanation:

The factored form of a polynomial is: a(x - p)(x-q)...(x-z) . where p, q, ..., z are the roots.

Convert the roots into factors, include conjugates of any complex roots, and multiply all of the factors. Then find the a-value.

roots: x = -2 x = 1 + i x = 1 - i (conjugate)

factors: x + 2 = 0 x - 1 - i = 0 x - 1 + i = 0

The polynomial has a degree of 4, so x = -2 must be a double root.

(x + 2)²(x - 1 - i)(x - 1 + i)

multiply the double root & complex roots:

(x² + 4x + 4)(x² - 2x + 2)

distribute (x² + 4x + 4) to find the basic polynomial

x⁴ + 8

Next, find the a-value:

P(x) = a(x⁴ + 8)

P(0) = a(0 + 8) = 4

8a = 4

`a=(1)/(2)`

`\boxed{P(x)=(1)/(2)(x^4+8)}`

***********************************************************************************

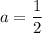
9. Answer: P(x) =
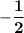`\bold{-(1)/(2)}`(x⁴ - x³ - 6x²)

Explanation:

The factored form of a polynomial is: a(x - p)(x-q)...(x-z) . where p, q, ..., z are the roots. The roots are where the graph crosses the x-axis.

roots: x = -2 x = 0 x = 3

factors: x + 2 = 0 x = 0 x - 3 = 0

The graph "touches - not crosses" the x-axis at x = 0 so x = 0 is a double root.

(x + 2)(x)²(x - 3)

multiply the factors (x + 2)(x - 3):

x²(x² - x - 6)

distribute (x)² to find the basic polynomial

x⁴ - x³ - 6x²

Next, find the a-value:

P(x) = a(x⁴ - x³ - 6x²)

P(2) = a[(2)⁴ -(2)³ - 6(2)²] = 8

a(16 - 8 - 24) = 8

-16a = 8

`a=-(1)/(2)`

`\boxed{P(x)=-(1)/(2)(x^4-x^3-6x^2)}`

***********************************************************************************

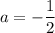
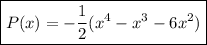
10. Answer: P(x) = -(x³ - 2x² + x - 2)

Explanation:

The graph displayed is an x³ graph that has been shifted to the left 2 units and reflected over the x-axis. Only one root is shown, which means the other two roots are complex numbers. Since P(i) = 0, then another root is: x = i

roots: x = -2 x = i x = - i (conjugate)

factors: x + 2 = 0 x - i = 0 x + i = 0

(x + 2)(x - i)(x + i)

multiply the complex roots:

(x + 2)(x² + 1)

distribute (x + 2) to find the basic polynomial

x³ - 2x² + x - 2

Next, reflect over the x-axis:

P(x) = - (x³ - 2x² + x - 2)