Question

`\tan( \alpha ) + 2\tan(2 \alpha ) + 4 \tan(4 \alpha ) + 8 \cot(8 \alpha ) = \cot( \alpha )`

Help plz​

Answer 1

I think proving a more general form will actually be easier than this specific case - it appears to be true that

`2^(n+1)\cot(2^(n+1)\alpha)+\displaystyle\sum_(i=0)^n2^i\tan(2^i\alpha)=\cot\alpha`

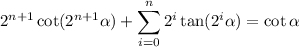
for
`n=0,1,2,3,\ldots`.

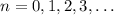Let's consider a proof by induction. The base case
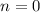`n=0` gives

`2\cot2\alpha+\tan\alpha=2(\cos2\alpha)/(\sin2\alpha)+(\sin\alpha)/(\cos\alpha)`

`=(\cos^2\alpha-\sin^2\alpha)/(\sin\alpha\cos\alpha)+(\sin\alpha)/(\cos\alpha)`

`=(\cos^2\alpha-\sin^2\alpha+\sin^2\alpha)/(\sin\alpha\cos\alpha)`

`=(\cos\alpha)/(\sin\alpha)=\cot\alpha`

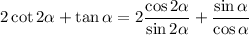
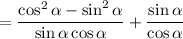
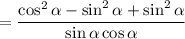
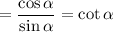
as desired.

Suppose the identity holds for
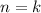`n=k`, so that

`2^(k+1)\cot(2^(k+1)\alpha)+\displaystyle\sum_(i=0)^k2^i\tan(2^i\alpha)=\cot\alpha`

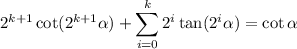
For
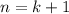`n=k+1`, we have

`2^(k+2)\cot(2^(k+2)\alpha)+\displaystyle\sum_(i=0)^(k+1)2^i\tan(2^i\alpha)`

`=2^(k+2)\cot(2^(k+2)\alpha)+2^(k+1)\tan(2^(k+1)\alpha)+\displaystyle\sum_(i=0)^k2^i\tan(2^i\alpha)`

`=2^(k+2)\cot(2^(k+2)\alpha)+2^(k+1)\tan(2^(k+1)\alpha)+(\cot\alpha-2^(k+1)\cot(2^(k+1)\alpha))`

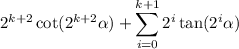
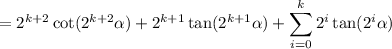
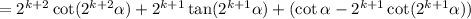
So we ultimately need to show that

`2^(k+2)\cot(2^(k+2)\alpha)+2^(k+1)\tan(2^(k+1)\alpha)-2^(k+1)\cot(2^(k+1)\alpha)=0`

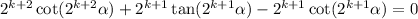
or

`2\cot(2^(k+2)\alpha)+\tan(2^(k+1)\alpha)=\cot(2^(k+1)\alpha)`

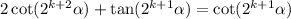
If we replace
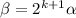`\beta=2^(k+1)\alpha`, we get(!) the base case, which we've shown to be true,

`2\cot2\beta+\tan\beta=\cot\beta`

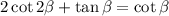
and thus the identity is proved.