Answer:
(a)
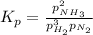
(b) (i)
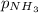 = 70.0 atm
= 70.0 atm
(ii) Kₚ = 3.58 × 10⁻³
(c) 69.4 mol
Step-by-step explanation:
3H₂ + N₂ ⇌ 2NH₃
(a) Kₚ expression
An equilibrium constant expression is always products/reactants, with each term raised to a power equal to its coefficient in the balanced equation. Thus
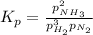
(b) Equilibrium values
(i) Ammonia
The total pressure became constant after 8 h, so the system was then at equilibrium.
We can use an ICE table to keep track of our calculations.
3H₂ + N₂ ⇌ 2NH₃
I/atm: 150.0 50.0 0
C/atm: -3x -x +2x
E/atm: 150.0-3x 50.0-x 2x
Initially, there was no ammonia present, so its partial pressure was zero.
Then, the H₂ and N₂ reacted until the system came to equilibrium.
How much reacted? We don't know. However, we are quite certain that x atm (some unknown quantity) of N₂ reacted, so its change in pressure was -x.
The molar ratios are 3:1:2, so 3x atm of H₂ must have disappeared (-3x) and 2x atm of ammonia must have formed (+2x).
Adding the changes to the initial values, we get the equilibrium values in the third line of the table.
What's the value of x? We don't know, but they tell us the total pressure at equilibrium.
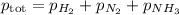
= (150.0 - 3x) + (50.0 - x) + 2x = 130.0
200.0 - 4x + 2x = 130.0
200.0 - 2x = 130.0 Subtract 130.0 from each side
70.0 - 2x = 0 Add 2x to each side
70.0 = 2x Divide each side by 2
x = 35.0 atm
Then, at equilibrium,
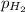 = (150.0 - 3x ) atm = (150.0 - 3×35.0) atm
= (150.0 - 3x ) atm = (150.0 - 3×35.0) atm
= (150.0 - 105.0) = 45.0 atm
 = (50.0-x) atm = (50.0-35.0) atm = 15.0 atm
= (50.0-x) atm = (50.0-35.0) atm = 15.0 atm
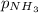 = 2 × 35.0 atm = 70.0 atm
= 2 × 35.0 atm = 70.0 atm
(b) (ii) Equilibrium constant
Kₚ = 70.0²/(45.0³×15.0)
= 4900/(91125 × 15.0)
= 4900/(1.367 × 10⁶)
= 3.58 × 10⁻³
(c) Moles of ammonia
We can use the Ideal Gas Law to calculate the moles of ammonia.
pV = nRT Divide each side by RT
n = (pV)/(RT)
= (70.0 × 50.0)/(0.082 06 × 615)
= 3500/50.47
= 69.4 mol