Question

If a hot steel tool of 1200°C was put in a bucket to cool and the bucket contained 15L of water of 15°C, and the water temperature rises to 48°C, how much would the mass of the tool in kg be?

(Q=m•c•∆T)
(c water = 4.18 J/g•°C) ​

Answer 1

3.6 kg.

Step-by-step explanation

How much heat does the hot steel tool release?

This value is the same as the amount of heat that the 15 liters of water has absorbed.

Temperature change of water:

`\Delta T = T_2 - T_1= 48\; \textdegree{\text{C}}- 15\; \textdegree{\text{C}} = 33 \; \textdegree{\text{C}}`.

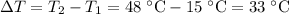Volume of water:

`V = 15 \; \text{L} = 15 \; \text{dm}^(3) = 15 * 10^(3) \; \text{cm}^(3)`.

Mass of water:

`m = \rho \cdot V = 1.00 \; \text{g} \cdot \text{cm}^(-3) * 15 * 10^(3) \; \text{cm}^(3) = 15 * 10^(3) \; \text{g}`.

Amount of heat that the 15 L water absorbed:

`Q = c\cdot m \cdot \Delta T = 4.18 \; \text{J} \cdot \text{g}^(-1) \cdot \textdegree{\text{C}}^(-1) * 15 * 10^(3) \; \text{g} * 33 \; \textdegree{\text{C}} = 2.06910 * 10^(6)\; \text{J}`.

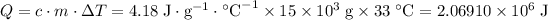What's the mass of the hot steel tool?

The specific heat of carbon steel is
`0.49 \; \text{J} \cdot \text{g}^(-1) \cdot \textdegree{\text{C}}^(-1)`.

The amount of heat that the tool has lost is the same as the amount of heat the 15 L of water absorbed. In other words,

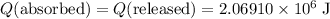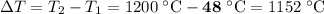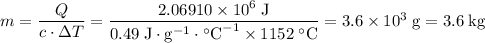`Q(\text{absorbed}) = Q(\text{released}) =2.06910 * 10^(6)\; \text{J}`.

`\Delta T = T_2 - T_1 = 1200\; \textdegree{\text{C}} -{\bf 48}\; \textdegree{\text{C}} = 1152\; \textdegree{\text{C}}`.

`m = (Q)/(c\cdot \Delta T) = \frac{2.06910 * 10^(6) \; \text{J}}{0.49\; \text{J} \cdot \text{g}^(-1) \cdot \textdegree{\text{C}}^(-1) * 1152\; \textdegree{\text{C}}} = 3.6 * 10^(3) \; \text{g} = 3.6 \; \text{kg}`.