Answer:
Maximum at (3, 23)
Explanation:
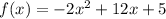
f(x)= a(x-h)^2 +k , where (h,k) is the vertex
Apply completing the square method to find vertex
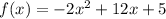
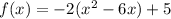
Let take half of coefficient of x is -6 divide by 2 is -3
square it (-3)^2 is 9
Add and subtract 9

Take out -9 and multiply by -2
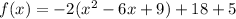
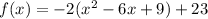
Now factor the parenthesis part
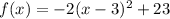
The value of h=3 and k=23
So vertex is (3,23)
The value of 'a' is -2, it means the parabola is upside down. so vertex is maximum
vertex is maximum at (3,23)