Question

Two identical billiard balls can move freely on a horizontal table. Ball a has a velocity V0 and hits balls B, which is at rest, at a point C defined by θ=45°. knowing that the coefficient of restitution between the two balls is e=0.8 and assuming no friction , determine the velocity of each ball after impact?

Answer 1

Velocity of ball B after impact is
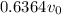`0.6364v_0` and ball A is
`0.711v_0`

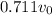
Step-by-step explanation:

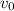`v_0` = Initial velocity of ball A

`v_A=v_0\cos45^(\circ)`

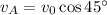
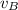`v_B` = Initial velocity of ball B = 0

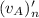`(v_A)_n'` = Final velocity of ball A

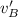`v_B'` = Final velocity of ball B

`e` = Coefficient of restitution = 0.8

From the conservation of momentum along the normal we have

`mv_A+mv_B=m(v_A)_n'+mv_B'\\\Rightarrow v_0\cos45^(\circ)+0=(v_A)_n'+v_B'\\\Rightarrow (v_A)_n'+v_B'=(1)/(√(2))v_0`

Coefficient of restitution is given by

`e=(v_B'-(v_A)_n')/(v_A-v_B)\\\Rightarrow 0.8=(v_B'-(v_A)_n')/(v_0\cos45^(\circ))\\\Rightarrow v_B'-(v_A)_n'=(0.8)/(√(2))v_0`

`(v_A)_n'+v_B'=(1)/(√(2))v_0`

`v_B'-(v_A)_n'=(0.8)/(√(2))v_0`

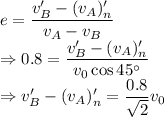
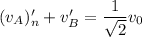
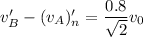
Adding the above two equations we get

`2v_B'=(1.8)/(√(2))v_0\\\Rightarrow v_B'=(0.9)/(√(2))v_0`

`\boldsymbol{\therefore v_B'=0.6364v_0}`

`(v_A)_n'=(1)/(√(2))v_0-0.6364v_0\\\Rightarrow (v_A)_n'=0.07071v_0`

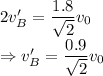
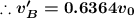
From the conservation of momentum along the plane of contact we have

`(v_A)_t'=(v_A)_t=v_0\sin45^(\circ)\\\Rightarrow (v_A)_t'=(v_0)/(√(2))`

`v_A'=√((v_A)_t'^2+(v_A)_n'^2)\\\Rightarrow v_A'=\sqrt{((v_0)/(√(2)))^2+(0.07071v_0)^2}\\\Rightarrow \boldsymbol{v_A'=0.711v_0}`

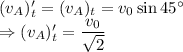
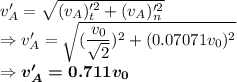
Velocity of ball B after impact is
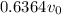`0.6364v_0` and ball A is
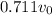`0.711v_0`.