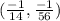Question

PLEASE HELP!!!! I DON'T KNOW THE ANSWERS!!

1)Which equation represents a parabola that has a focus of (0, 0) and a directrix of y = 4?

x2=−8(y−2)
x2=−2y ​
x2=−8y
x2=−2(y−2) ​


2)What is the vertex of the parabola?

y−3=12(x+5)2

Enter your answer in the boxes.


3)What is the focus of the parabola?

y=−14x2−2x−2

Enter your answer in the boxes.

Answer 1

Part 1). Given Point of focus = ( 0 , 0 ) and equation of directrix, y = 4

Distance from parabola focus to its highest point is same as from its highest point to its directrix so it's highest point must be (0,2).

Distance from focus to its point of intersection with x-axis is same as distance from that point to directrix so points of intersection with x-axis are (-4,0) and (4,0).

Thus this parabola equation gotta be

y = 2 - kx²

Put, y=0 at x=4:

0 = 2 - k × 16

k = 1/8

Thus, Equation of Parabola,

y = 2 - (1/8)x²

x² = -8 ( y -2 )

Therefore, Option A is correct.

Part 2).

Given Equation of parabola , y - 3 = 12 ( x + 5 )²

We have to find vertex of the parabola,

by comparing with the standard form,

( x - h )² = 4a ( y - k )

( x + 5 )² = (1/12) ( y - 3)

Therefore, Vertex ( h , k ) = ( -5 , 3 )

Part 3).

Given Equation of parabola , y = -14x² - 2x - 2

We have to find focus of the parabola,

by comparing with the standard form,

( x - h )² = 4a ( y - k )

Focus is ( h , a )

y = -14x² - 2x - 2

`y=-14(x+(1)/(14))^2-(27)/(14)`

`y+(27)/(14)=-14(x+(1)/(14))^2`

`(x+(1)/(14))^2=(-1)/(14)(y+(27)/(14))`

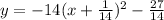
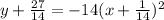
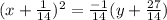
Now,
`4a=(-1)/(14)`

`a=(-1)/(56)`

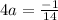
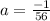
So, Focus =
`((-1)/(14),(-1)/(56))`