Question

Jennifer is wrapping presents. One of the rectangular gift boxes has dimensions 1 in. • 7 in. • 3 in. and the other has dimensions 2 in. • 7 in. • 9 in. How much wrapping paper will she need to wrap both gifts in total? Explain;)

Answer 1

Total amount of wrapping required = 252 inch²

Explanation:

Dimensions of the 1st box are given by,

Length = 1 inch, Width = 7 inch and Height = 3 inch

As, Surface area of a rectangular box =
`2(Length* Width+Length* Height+Height* Width)`

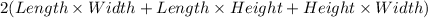
So, Surface area of the 1st box =
`2(1* 7+1* 3+3* 7)`

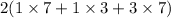
i.e. Surface area of the 1st box =
`2(7+3+21)`

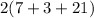
i.e. Surface area of the 1st box = 2 × 31 = 62 inch²

Further, we have,

Dimensions of the 2nd box are given by,

Length = 2 inch, Width = 7 inch and Height = 9 inch

So, Surface area of the 2nd box =
`2(2* 7+2* 9+9* 7)`

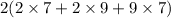
i.e. Surface area of the 2nd box =
`2(14+18+63)`

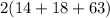
i.e. Surface area of the 2nd box = 2 × 95 = 190 inch²

Thus, the total amount of wrapping required = 62 + 190 = 252 inch².