Question

The triangles shown are similar. Which angle corresponds to angle E?

A) ∠P
B) ∠Q
C) ∠R
D) ∠D

Two similar rectangles are shown. Which statement is true?
A) The area of rectangle B is
1
3
the area of rectangle A.
B) The area of rectangle B is
1
9
the area of rectangle A.
C) The area of rectangle B is nine times the area of rectangle A.
D) The area of rectangle B is three times the area of rectangle A.

Which pair of rectangles are similar?
A) A and B
B) A and D
C) A and F
D) A and G

Answer 1

The solution is ∠P. If you rotate triangle DEF so that it is oriented the same way as triangle PQR, you can see that angle E corresponds to angle P.

Answer 2

2) Option A

3) Option C

5) Option D

Explanation:

2) In two similar triangles shown PQR and DEF all corresponding sides will be in the same ratio.

`(EF)/(PQ)=(DF)/(QR)=(DE)/(PR)`

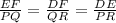
Similarly angles opposite to the corresponding sides in congruent triangles will be equal which shows

∠E = ∠P

Option A is the correct answer.

3). If the given rectangles are similar then sides of the rectangles will be in

the same ratio.

Then area of A = 1×2 =2

and area of B = 3×6 =18

Ratio of the area of A and B = 2/18 = 1/9

area of B = 9A

So option C is the correct answer.

5). In this part we will count the number of small squares at the background of each rectangle.

For rectangle A sides are 4 and 8.

For rectangle B sides are 3 and 4.

For C sides are 3 and 6.

For D sides are 2 and 5.

For E sides are 2 and 4.

For F sides are 2 and 3.

For G sides are 1 and 2.

For H sides are 1 and 3.

Now as per options given pair A and G are similar as the ratio of their sides are same.

A/G = 2/1

Therefore Option D is the answer.