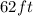Answer: 62 feet approximately.
Step-by-step explanation:
1. Based on the information given in the problem, you can draw a right triangle as the one shown in the image attached, where the height of the tent is represented with
 . Therefore, you can calculate it as following:
. Therefore, you can calculate it as following:

Where:

2. Substitute values and solve for
 , then the height of the circus tent is:
, then the height of the circus tent is:

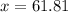 ≈
≈