Question

You are on a boat in the ocean at point A. You locate a lighthouse at point D, beyond the line of sight of the marker at point C. You travel 90 feet west to point b and then 36 feet south to point C. You travel 100 feet more to arrive point E, which is due east of the lighthouse. What is the distance from point E to the lighthouse?

Answer 1

Answer: The distance from point E to the lighthouse = 250 feet

Explanation:

Since, after making the diagram of this situation,

We get two triangles ABC and CED,

In which AB = 90 feet, BC = 36 feet and CE = 100 feet,

Now,

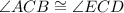`\angle ACB\cong \angle ECD` ( Vertically opposite angles )

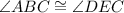`\angle ABC\cong \angle DEC` ( Right angles )

By AA similarity postulate,

`\triangle ABC\sim \triangle DEC`

By the property of similar triangles,

`(AB)/(ED)=(BC)/(EC)`

`(90)/(ED)=(36)/(100)`

`9000=36DE`

`250=DE`

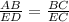
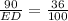
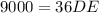
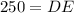
Since, point D represents the lighthouse.

Hence, the distance from point E to the lighthouse = 250 feet