Answer:
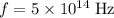 if the wavelength is observed in vacuum.
if the wavelength is observed in vacuum.
Explanation:
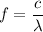 ,
,
where
 is the frequency of this beam of light,
is the frequency of this beam of light,
 is its wavelength, and
is its wavelength, and
 is the speed of light.
is the speed of light.
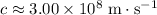 in vacuum and in the earth atmosphere. However, the value of
in vacuum and in the earth atmosphere. However, the value of
 will be smaller in other media.
will be smaller in other media.
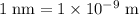 .
.
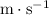 is the SI unit for speed.
is the SI unit for speed.
 is the SI unit for distance.
is the SI unit for distance.
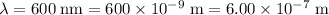 .
.
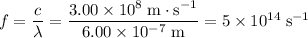 .
.
One [oscillation] in each second is the same as one Hertz
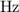 . In other words,
. In other words,
 .
.
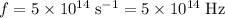 .
.