Answer: Option A.
Explanation:
1. By definition the law of cosine is:
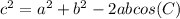
2. By definition, the angle
 is opposite to the side whose length is
is opposite to the side whose length is
 .
.
3. Then, as you can see in the figure attached in the problem the length of the side c is:

3. Therefore, you can conclude that the measure of the angle
 is 67°.
is 67°.
4. To verify you can solve for the angle, as following:
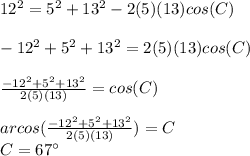
Then, the answer is the option A.