Question

First term: 2 3/4 sixth term: 3 7/12 what is the rule

Answer 1

we conclude that the rule will be:

`a_n=(31)/(12)+(1)/(6)n`

Explanation:

Given

`a_6=3(7)/(12)=(43)/(12)`

`a_1=2(3)/(4)=(11)/(4)`

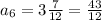
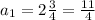
We know the arithmetic sequence with the common difference is defined as

`a_n=a_1+\left(n-1\right)d`

where a₁ is the first term and d is a common difference.

so

a₆ = a₁ + (6-1) d

substituting a₆ = 43/12 and a₁ = 11/4 to determine d

`(43)/(12)=\:(11)/(4)\:+\:5d`

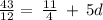
switch sides

`(11)/(4)+5d=(43)/(12)`

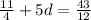
subtract 11/4 from both sides

`(11)/(4)+5d-(11)/(4)=(43)/(12)-(11)/(4)`

`5d=(5)/(6)`

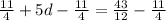
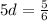
Divide both sides by 5

`(5d)/(5)=((5)/(6))/(5)`

`d=(1)/(6)`

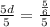
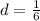
as

a₁ = 11/4

`d=(1)/(6)`

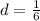
Therefore, the nth term of the Arithmetic sequence will be:

`a_n=a_1+\left(n-1\right)d`

substituting d = 1/6 and a₁ = 11/4

`a_n=(11)/(4)+\left(n-1\right)(1)/(6)`

`=(11)/(4)+(1)/(6)n-(1)/(6)`

`=(31)/(12)+(1)/(6)n`

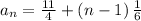
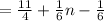
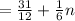
Therefore, we conclude that the rule will be:

`a_n=(31)/(12)+(1)/(6)n`