Question

A gigantic balloon used for a parade is shaped like an ice cream cone. The radius of the cone and the hemisphere is 12 feet. The height of the cone is 60 feet. If the balloon with helium at the rate of 70 cubic feet per minute, about how many minutes fill the balloon? Round each volume to the nearest tenth of a cubic foot, Round the time to the nearest minute.

Volume of hemisphere_____
Volume of cone____
Total volume____
Time to fill the balloon____

Answer 1

Volume of hemisphere: 10,851.84

Volume of cone: 9,043.2

Total volume: 19,895.04

Time to fill the balloon: 284 minutes

Explanation:

To find the time, calculate the volume divide it by the rate 70 cubic feet per minute.

The volume of a cone is found using the volume formula for a cone
`V=(1)/(3)\pi r^2h`.

Substitute h=60 and r = 12.

`V = (1)/(3)\pi r^2h\\V = (1)/(3)\pi (12^2)(60)\\V=(1)/(3)\pi *144*60\\V = (8640)/(3)\pi \\V= 2880\pi = 9,043.2`

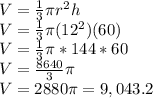
The volume of a hemisphere is half of the volume of a sphere
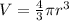`V=(4)/(3)\pi r^3`. Substitute r=12.

`V=(4)/(3)\pi r^3\\V=(4)/(3)\pi 12^3\\V=(4)/(3)\pi *1728\\V=(4*1728)/(3)\pi\\ V=6912\pi = 21,703.68`

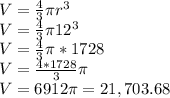
However the hemisphere is half this so it is
`10,851.84`.

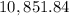Together the volume is 10,851.84 + 9,043.2 = 19,895.04

Divide this by 70 and the float fills up in 284 minutes.