Answer:
A and D are not polynomials. B and C are polynomials
Explanation:
In order to find out what function is a polynomial, you have to understand what a polynomial is. A polynomial is a sum of monomials that make up a polynomial expression. A mononomial is a real number, with a variable, and a exponent of a variable that makes up one term. For example
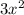 is a monomial. It has a real number, a variable, and a exponent that makes up one term. A polynomial has one or more monomial terms that make it a polynomial. So firstly, a polynomial by definition cannot have a negative exponent. That eliminates D. Why? because by definition, the standard form of a polynomial function states that n cannot be positive, it has to be a nonnegative integer. Also, polynomials can only be real numbers. It cannot have a nonreal number. Radical forms without a perfect square are nonreal numbers. So that eliminates A. However, B and C can be polynomials because the definition of polynomials say that real numbers, nonnegative exponents, and constants can be part of a polynomial function. Even with the fraction, that would be part of rational expressions (polynomial/polynomial), which is polynomials. I hope this helps friend. Math can be tough to explain just as much as doing it :)
is a monomial. It has a real number, a variable, and a exponent that makes up one term. A polynomial has one or more monomial terms that make it a polynomial. So firstly, a polynomial by definition cannot have a negative exponent. That eliminates D. Why? because by definition, the standard form of a polynomial function states that n cannot be positive, it has to be a nonnegative integer. Also, polynomials can only be real numbers. It cannot have a nonreal number. Radical forms without a perfect square are nonreal numbers. So that eliminates A. However, B and C can be polynomials because the definition of polynomials say that real numbers, nonnegative exponents, and constants can be part of a polynomial function. Even with the fraction, that would be part of rational expressions (polynomial/polynomial), which is polynomials. I hope this helps friend. Math can be tough to explain just as much as doing it :)