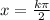Question

is the function f(x)= sec x and g(x)= sin x, what is the composed function f(g(x)= sec(sin x) and what are its domain and range?

Answer 1

1. B f(x)=4sinx/2-3

2. B, F, G (c=-1. a=2, b=2)

3. c. H(t)=-2.4cos(0.017t)+12

4. A, B, E, F (y=cos^-1x, y=cot^-1x, y=sin^-1x, y=tan^-1x)

5. C y=sin^-1x

6. C 48.7

7. C f(g(x))=sec(sinx) domain: all real #

8. C step 3

Explanation:

Answer 2

f(g(x)) = sec(sin(x)) Third option

Explanation:

In this problem we have 2 functions:

g(x) = sin(x)

f(x) = sec(x)

Where sec(x) = 1/cos(x)

Then we find f (g (x)) by introducing the function g into the function f.

The result is as follows:

f(g(x)) = sec(sin(x))

We know that the domain of the sec(x) are all values of x of the form
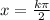`x = (k\pi)/(2)` where k is an odd integer.

On the other hand the domain of sin(x) are all real numbers.

Then the domain of f(g(x)) must be all values of x such that sin(x) is different from
`x = (k\pi)/(2)`

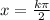
Sin(x) is never equal to
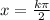`x = (k\pi)/(2)`. Therefore the domain of f(g(x)) are all real numbers, and its rank is
`1 \leq x\leq 1.85`

Where 1.85 is the maximum value that reaches when
`x = (k\pi)/(2)`