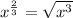Question

Rewrite in simplest radical form x^ 5/6 over x^ 1/6 show each step of your process

Answer 1

Answer:
`\bold{\sqrt[3]{x^2} }`

Explanation:

`\frac{x^{(5)/(6)}}{x^{(1)/(6)}}\\\\\\=x^{(5)/(6)-(1)/(6)}}}\\\\\\=x^{(4)/(6)}}}\\\\\\=x^{(2)/(3)}}}\\\\=\sqrt[3]{x^2}`

Answer 2

The simplest Radical =
`\sqrt{x^(3) }`

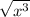
Explanation:

The two terms of the fraction are
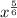`x^{(5)/(6)}`⇒numerator

and
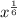`x^{(1)/(6)}`⇒denominator

Both of them are same variable x

So we can use the rule of the power:

If we divide to terms have the same base we subtract their powers

`\frac{x^{(5)/(6) } }{x^{(1)/(6) } }=x^{(5)/(6)-(1)/(6)  }=x^{(4)/(6) } =x^{(2)/(3) }`

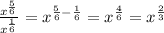
If the power is in the shape of fraction so the numerator of the fraction represents the radical and the denominator represents the power inside the radical.

`x^{(2)/(3) }=\sqrt{x^(3) }`