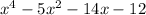Answer:
(a)
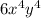
(b)
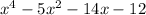
Explanation:
(a)
(3xy^3)(2x^3y)
- (3*2)(x*x^3)(y*y^3)
- (6)(x^4)(y^4)
(b)
This is just the rainbow method or as i like to call it the multiplication attack. All the terms in the first bracket fire themselves on the ones in the second. Each term attacks all the other terms once. Once they fire (multiply) they stick and can be added up. To make it easier i like to imagine them as squads.
(x^2 +2x +3)[x^2 -2x-4]
This can be expressed now as
(x^2 +2x +3)[x^2] + (x^2 +2x +3)[-2x] + (x^2 +2x +3)[-4]
Now to expand
x^4 + 2x^3 + 3x^2 -2x^3 -4x^2 - 6x -4x^2 - 8x - 12
Group like terms (same x powers)
(x^4) + (2x^3-2x^3) + (3x^2-4x^2-4x^2) + (- 6x-8x) + (-12)
Simplify