Question

The frozen The yogurt cone shown is made from a cone and a hemisphere. radius is 6 cm. Th e total height of the figure is 24 cm. Suppose the cone is completely packed with frozen yogurt.

The height of the cone is_____cm

The height of the hemisphere is_____cm

The exact volume of the cone is ____ pi cm^3

The exact volume of the hemisphere is ____pi cm ^3

Answer 1

The height of the cone is 18 cm, the height of the hemisphere is 6 cm, the exact volume of the cone is 226.368 pi cm^3, and the exact volume of the hemisphere is 452.736 pi cm^3.

Step-by-step explanation:

To find the height of the cone, we can subtract the height of the hemisphere from the total height of the figure: height of cone = total height - height of hemisphere = 24 cm - 6 cm = 18 cm.

The volume of a cone is given by the formula V = πr^2h/3, where r is the radius and h is the height. Plugging in the values, we get: exact volume of the cone = 3.142 × (6 cm)^2 × 18 cm / 3 = 226.368 cm^3.

The volume of a hemisphere is given by the formula V = 2πr^3/3, where r is the radius. Plugging in the values, we get: exact volume of the hemisphere = 2 × 3.142 × (6 cm)^3 / 3 = 452.736 cm^3.

Answer 2

The height of the cone is 18 cm

The height of the hemisphere is 6 cm

The exact volume of the cone is 216 pi cm^3

The exact volume of the hemisphere is 144 pi cm ^3

Step-by-step explanation:

Since the height of the entire figure is 24 then the height of the cone is 18 cm. This is true since a hemisphere is half a sphere and its height will be its radius which is 6. The height if the hemisphere is 6. So 24 - 6 = 18, the height of the cone.

The volume of the cone is found using the volume formula for a cone
`V=(1)/(3)\pi r^2h`.

Substitute h=18 and r = 6.

`V = (1)/(3)\pi r^2h\\V = (1)/(3)\pi (6^2)(18)\\V=(1)/(3)\pi *36*18\\V = (648)/(3)\pi \\V= 216\pi`

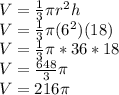
The volume of a hemisphere is half of
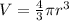`V=(4)/(3)\pi r^3`. Substitute r=6.

`V=(4)/(3)\pi r^3\\V=(4)/(3)\pi 6^3\\V=(4)/(3)\pi *216\\V=(4*216)/(3)\pi\\ V=288\pi`

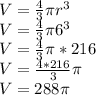
However the hemisphere is half this so it is
`144\pi`.