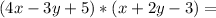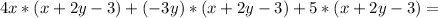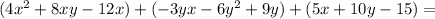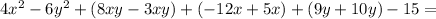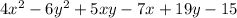Question

Which of the following polynomials corresponds to the product of the multivariate polynomials 4x - 3y + 5 and x + 2y -3?

5x - y + 2
4x 2 - 6y 2 - 15
4x 2 + 8xy - 12x - 3y + 5
4x 2 - 6y 2 + 5xy - 7x + 19y - 15

Answer 1

`4x^2 - 6y^2 + 5xy - 7x + 19y - 15`

Explanation:

Let's solve the problem, but first remember the following:

when you are going to multiply two polynomials each of them involving several terms, then the multiplication is the sum of multiplying each term from the first polynomial by each of the terms of the second one.

In your practical exercise this means the following:

`(4x-3y+5)*(x+2y-3)=`

`4x*(x+2y-3) + (-3y)*(x+2y-3) + 5*(x+2y-3)=`

`(4x^2+8xy-12x) + (-3yx-6y^2+9y) + (5x+10y-15)=`

`4x^2 - 6y^2 + (8xy-3xy) + (-12x+5x) + (9y+10y) - 15=`

`4x^2 - 6y^2 + 5xy - 7x + 19y - 15`