Answer:
P(A | Y = 8) = 0.633
Explanation:
It is really a simple and interesting question, as it involves the Poisson distribution and probability.
First of all, let's try to understand the problem statement clearly. It says that there are two process by which beams are made, namely A and B.
It further states that, beam made by process A has = 10 flaws per meter.
Beam made by process B has = 5 flaws per meter.
Finally, it says that from a yard containing equal numbers of process A and process B beans, one beam is randomly selected and 1 - meter of it is inspected. And they have found 8 flaws in it.
We now, have to find out the probability that the inspected beam is from process A.
For this,
Let's suppose, Y is no. of flaws
So,
P (Y=8|A) =
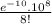
where , e = Euler's Constant = 2.71828
P (Y=8|A) = 0.11
Similarly for process B
P (Y=8|B) =
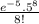
P (Y=8|B) = 0.06
As, we know from the problem statement that there are equal numbers of process A and process B beams.
So, the probability of A = Probability of B = 0.5
P(A) = 0.5
P(B) = 0.5
We need to find, P(A|Y=8) and for this we need to find the P(Y=8) first.
Using the law of total probability:
P(Y=8) = P(Y = 8 |A) P(A) + P(Y = 8|B) P(B)
Plug in the values:
P(Y=8) = (0.11 x 0.5) + (0.06 x 0.5)
P(Y=8) = 0.088
Now, by applying Bayes Theorem, we can find the required probability:
P(A | Y = 8) = P(Y = 8 | A) P(A) / P(Y = 8)
8 flaws are found, the probability the inspected beam was fabricated using process A is :
P(A | Y = 8) = 0.11 x 0.5 / 0.088
P(A | Y = 8) = 0.633
Furthermore,
8 flaws are found, the probability the inspected beam was fabricated using process B is :
P(B | Y = 8) = 1-P(A | Y = 8)
P(B | Y = 8) = 1 - 0.633
P(B | Y = 8) = 0.367