Answer:
second option

Explanation:
We have a function of the form

We know that the cos(x) function is periodic.
That's why
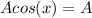 when
when
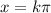
Where k is an even number.
Also
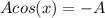 when
when
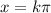
Where k is an odd integer.
Finally
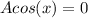 when
when
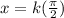 and k is an odd integer.
and k is an odd integer.
With this information we can evaluate the options given for the function f(x) with the values presented in the attached table and see which one is more similar.
For example, for the point (0, 25) we have Acos(0) = A.
Then A + h = 25
Of the options presented, the one that best approximates this result is:

Because:
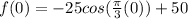
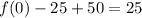
If we try another point, for example (3, 75) we have:
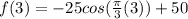
We know that
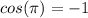
So:

In point (6, 26) we have:
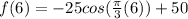

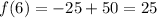
Finally the answer is the second option