The period of the same pendulum will be longer on Mt. Everest than somewhere closer to the ground.
Step-by-step explanation
Let
 be the period of this simple pendulum,
be the period of this simple pendulum,
 the length of the rod holding the pendulum, and
the length of the rod holding the pendulum, and
 the gravitational field strength at the point of the pendulum.
the gravitational field strength at the point of the pendulum.
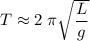 if the pendulum swings at small angles. In other words, reducing the value of
if the pendulum swings at small angles. In other words, reducing the value of
 increases the length of the period.
increases the length of the period.
How does the value of
 compare on Mt. Everest and at sea level?
compare on Mt. Everest and at sea level?
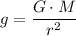 ,
,
where
 is the gravitational field strength,
is the gravitational field strength,
 the mass of the planet earth,
the mass of the planet earth,
 the distance away from the center of the earth, and
the distance away from the center of the earth, and
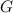 is a constant.
is a constant.
 is at the denominator. A large value of
is at the denominator. A large value of
 will lead to a small value of
will lead to a small value of
 . Mt. Everest is further away from the center of the earth than a spot at sea level. As a result,
. Mt. Everest is further away from the center of the earth than a spot at sea level. As a result,
 will be larger at the sea level and smaller on top of Mt. Everest.
will be larger at the sea level and smaller on top of Mt. Everest.
Now, back to the approximation
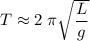 .
.
The value of
 is smaller on Mt. Everest than at sea level. As a result, the time period of the pendulum
is smaller on Mt. Everest than at sea level. As a result, the time period of the pendulum
 will be larger on Mt. Everest than at sea level.
will be larger on Mt. Everest than at sea level.