Answer:
Explanation:
Equation of the quadratic function given as,
g(x) =
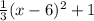
Since, leading coefficient of the function is positive,
Parabola will open upwards.
For x- intercepts,
g(x) = 0
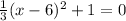
(x - 6)² = -3
(x - 6) = ±√(-3)
x = 6 ± √(-3)
Since, x is an imaginary number, this function has no x-intercepts.
Similarly, for y-intercept,
x = 0
g(0) =
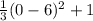
= 12 + 1
= 13
y-intercept of the function → y = 13
Vertex of the parabola → (6, 1)
For x = 12,
g(12) =
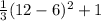
= 13
Therefore, one point lying on the graph will be (12, 13).
Now we can graph the quadratic function given in the question.