Answer: 0.3
Explanation:
From the given table, the probability that a person chosen at random, who lives in the city, lives in the East =
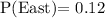
The probability that a person chosen at random, who lives in the city, lives in the West =
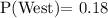
Since all the vents are independent .
Then, the probability that a person chosen at random, who lives in the city, lives in the East or West region is given by :-

Hence, the probability that a person chosen at random, who lives in the city, lives in the East or West region =0.3