Question

A particle with charge 8 µC is located on the

x-axis at the point −10 cm , and a second
particle with charge −3 µC is placed on the
x-axis at 10 cm .
What is the magnitude of the total electrostatic force on a third particle with charge
−7 µC placed on the x-axis at 2 cm ? The
Coulomb constant is 8.9875 × 109 N · m2
/C
2
.
Answer in units of N.

Answer 1

The magnitude of the total electrostatic force on the third particle is approximately 0.7917 N.

Step-by-step explanation:

To calculate the magnitude of the total electrostatic force on a third particle with charge -7 µC, we can use Coulomb's law. The formula for Coulomb's law is:

F = k * (q1 * q2) / r^2

where F is the electrostatic force, k is the Coulomb constant (8.9875 x 10^9 N · m^2 / C^2), q1 and q2 are the charges, and r is the distance between the charges.

Applying this formula to the given information, we have:

F = (8.9875 x 10^9 N · m^2 / C^2) * ((8 µC) * (-7 µC)) / (0.02 m)^2

Simplifying the equation, we find that the magnitude of the total electrostatic force on the third particle is approximately 0.7917 N.

Answer 2

Answer: 34.65 N towards charge 8 μC.

Step-by-step explanation:

The electrostatic force between two charges is given by:

`F =k (q_1q_2)/(r^2)`

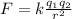
where, k is the Coulomb constant = 8.9875 × 10⁹ N.m²/C²

q₁ and q₂ are the two charges separated by distance r.

The distance between charges 8 μC and -7 μC is r = 2 cm -(-10 cm) = 12 cm = 0.12 m

The force between these charges is:

`F = 8.9875 * 10^9 Nm^2/C^2 * (8* 10^(-6)C* (-7*10^(-6)C))/((0.12m)^2) = -34.95 N`

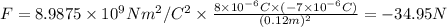
Negative sign implies it is an attractive force.

The distance between -3 μC charge and -7 μC charge is r' = 10 cm -2 cm = 8 cm = 0.8 m.

The electrostatic force between these charges is:

`F' = 8.9875* 10^9Nm^2/C^2* ((-3 * 10^(-6)C)* (-7* 10^(-6)C))/((0.8m)^2) = 0.295 N`

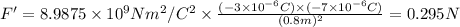
It is a repulsive force.

Net force on the -7 μC charge is:

Fn = F + F'

we can add them directly as they are acting in one direction along the x-axis.

Fn = -34.95 N + 0.295 = -34.65 N

Thus, the net force is attractive in nature and it is towards charge 8 μC.