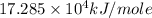Question

He rate constant of a reaction is 4.55 × 10−5 l/mol·s at 195°c and 8.75 × 10−3 l/mol·s at 258°c. what is the activation energy of the reaction? enter your answer in scientific notation.

Answer 1

Answer;

139.8 kJ/mol

Step-by-step explanation;

The activation energy is given by the formula;

Eₐ = R•ln[k₂/k₁]•T₁T₂/(T₂ – T₁)

After converting ˚C to K:

T1 = 531 K

T2 = 468 k (after converting ˚C to K):

R = 8.314 J/mol•K

Eₐ = (8.314 J/mol•K) × ln[(3.2 × 10⁻³)/(4.5 × 10⁻⁵)] × (531 K)(468 K)/(531 – 468 K)

Eₐ = 139.8 kJ/mol

Answer 2

Answer : The activation energy of the reaction is,
`17.285* 10^4kJ/mole`

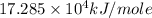
Solution :

The relation between the rate constant the activation energy is,

`\log (K_2)/(K_1)=(Ea)/(2.303* R)* [(1)/(T_1)-(1)/(T_2)]`

where,

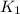`K_1` = initial rate constant =
`4.55* 10^(-5)L/mole\text{ s}`

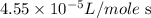
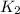`K_2` = final rate constant =
`8.75* 10^(-3)L/mole\text{ s}`

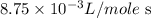
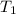`T_1` = initial temperature =
`195^oC=273+195=468K`

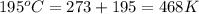
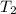`T_2` = final temperature =
`258^oC=273+258=531K`

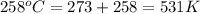
R = gas constant = 8.314 kJ/moleK

Ea = activation energy

Now put all the given values in the above formula, we get the activation energy.

`\log \frac{8.75* 10^(-3)L/mole\text{ s}}{4.55* 10^(-5)L/mole\text{ s}}=(Ea)/(2.303* (8.314kJ/moleK))* [(1)/(468K)-(1)/(531K)]`

`Ea=17.285* 10^4kJ/mole`

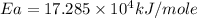
Therefore, the activation energy of the reaction is,
`17.285* 10^4kJ/mole`