Question

Maximize: z=6x + 4y

subject to: 8x - y lesser or equal to 15
3x + y greater or equal to 10
x greater or equal to 2
x lesser or equal to 8
use graphical methods to solve
The maximum value is 50
(Type an integer or simplified fraction.)

Answer 1

The maximum value of z is 244 at x= 8 and y=49.

Explanation:

We are given the system of equations as,

Maximize :
`z= 6x+4y`

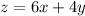
Subject to :
`8x-y\leq 15`

`3x + y\geq 10`

`x\geq 2`

`x\leq 8`

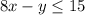
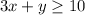
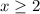
After plotting the inequalities to which the maximized function is subjected to, we get the following graph.

So, we will find the value of 'z' at the enclosing the solution region.

`z= 6x+4y`

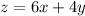
(2,4) z= 6×2+4×4= 12+16 = 28

(2.273,3.182) z= 6×2.273+4×3.182 = 13.64+12.73= 26.37

(8,49) z= 6×8+4×49 = 48+196= 244

Thus, we get that the maximum value of z is 244 at x= 8 and y=49.