Answer:
The value of n is 21
Explanation:
The series is 19 , 15 , 11 , ............
It has a constant difference between each two consecutive terms, so it is an arithmetic series.
The rule of the sum of n terms in the arithmetic series is:
![S_(n)=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2020/formulas/mathematics/high-school/18ly1pcix4xprbsf3lks1jjup3948pknar.png)
Where a is the first term of the series , d is the difference between each two consecutive terms and n is the number of the terms in this series
So from the series above:
a = 19 , d = 15 - 19 = -4 ( it must be second term - first term ) ,
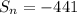
![-441=(n)/(2)[2(19)+(n-1)(-4)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/d6fwvjs8vfyco4hsb5i6582enqb8yba8we.png)
![-441=(n)/(2)[38+(-4n+4)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/83dpnaazqqlgpw77bbyl0x0epajowongfp.png)
![-441=(n)/(2)[38-4n+4]](https://img.qammunity.org/2020/formulas/mathematics/high-school/dj4v0xzadi6c1po7dx0catwjcrizam35oq.png)
![-441=(n)/(2)[42-4n]](https://img.qammunity.org/2020/formulas/mathematics/high-school/8alazdav25npyk61avgd0rixcxb2ebko1a.png)
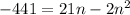
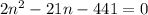 ⇒Use factorization
⇒Use factorization
(2n + 21) (n - 21) = 0
2n + 21 = 0 ⇒ 2n = -21 ⇒ n = -21/2⇒Not accepted n must be positive integer
n - 21 = 0⇒ n = 21
∴-441 is the sum of 21 terms in this series