Answer:
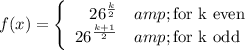
Explanation:
Half the length of the palindrome can be any possible sequence of the 26 available letters. The other half is constrained to be the reverse of the same sequence. For odd length sequences, the middle letter can be any of the 26.
So, for k even, the number of palindromes is 26^(k/2). For k odd, the number is 26·26^((k-1)/2) = 26^)((k+1)/2).