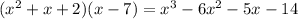Question

P( x) =x^3-6x^2-5x-14 What is the remainder R when the polynomial p(x) is divided by (x-7)

Answer 1

The remainder is zero

Explanation:

To find the remainder we will use the long division

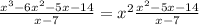`(x^(3)-6x^(2)-5x-14)/(x-7)=x^(2)(x^(2)-5x-14 )/(x-7)`⇒(1)

`(x^(2)-5x-14)/(x-7)=x(2x-14)/(x-7)`⇒(2)

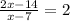`(2x-14)/(x-7)=2`⇒(3)

From (1) , (2) and (3)

The quotient of the long division is
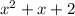`x^(2)+x+2` and no remainder

So the remainder is zero

* If you want to check your answer Multiply the quotient by the divisor

`(x^(2)+x+2)(x-7)=x^(3)-6x^(2)-5x-14`