Answer:
B: Permutation; Number of ways = 60
Explanation:
First we have to decide if this is a problem of permutation or combination. The rule is:
- If the order matters, permutations will be used
- If order does not matter, combinations will be used
In this problem, they order of awarding the medals matters, so this is a permutation problem.
We have to award 3 medals among 5 runners. So this can be done in 5P3 ways:
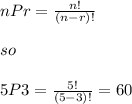
Therefore, there are 60 ways to award the medal. Therefore, the correct answer is B.