Question

Solve the following system of equations for x : y=4-x2 x-y=2

a. x= 2,-4
b. x= 2,-3
c. x= -2,4
d. x= -3

Answer 1

b. x=2, -3

Explanation:

So I'm assuming the two equations are:
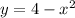`y=4-x^2` and
`x-y=2`

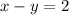
Since it's asking to solve to solve for x. Then we need to solve for y in one of the equations, so that's it's defined using x, then substitute that into the other equation, that way the only variable left is going to be the x variable.

So since y is already solved for in the first equation. I'll plug that into the second equation.

Original equation:

`x-y=2`

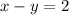
Substitute 4-x^2 in as y

`x-(4-x^2)=2`

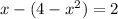
Distribute the negative sign

`x-4+x^2=2`

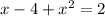
Organize it so it's in order by degree

`x^2+x-4=2`

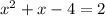
Subtract 2 from both sides

`x^2+x-6=0`

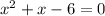
So now we have a quadratic equation and we're trying to find the zeroes. You can use the quadratic equation, but since the only options are integers, we can easily factor this equation. So you need to look for factors of -6, which add up to 1. I like to think about it as find two numbers with a difference of 1, and then figure out which is going to be positive and which is going to be negative after. So knowing this you can easily see 3 and 2 have a difference of 1. Since the 1 is positive, that means the 3 has to be positive and the 2 has to be negative

Use the factors: 3 and -2 to rewrite the equation:

`(x+3)(x-2)`

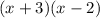
Now set each factor equal to 0

x+3 = 0

x=-3

x-2=0

x=2

this gives you the two solutions: -3, and 2