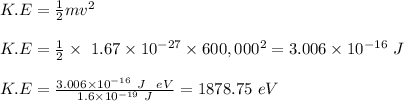Question

A proton with an initial speed of 600,000 m/s is brought to rest by an electric field.1. What was the potential difference that stopped the proton?

2. What was the initial kinetic energy of the proton, in electron volts?

Answer 1

(1) the potential difference that stopped the proton is 1878.75 V

(2) the initial kinetic energy of the proton is 1878.75 eV

Step-by-step explanation:

Given;

initial speed of the proton, v = 600,000 m/s

mass of proton, m = 1.67 x 10⁻²⁷ kg

(1) The work done in bringing the proton to rest is given as;

`W = eV`

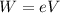
Apply work energy theorem;

`K.E =W\\\\ (1)/(2) mv^2 = eV\\\\V = (mv^2)/(2e)`

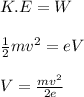
where;

V is the potential difference

`V = (1.67* 10^(-27) *\ 600,000^2)/(2 \ * \ 1.6 * 10^(-19)) \\\\V = 1878.75 \ V`

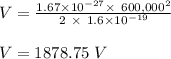
(2) the initial kinetic energy of the proton, in electron volts;

`K.E = (1)/(2) mv^2\\\\K.E = (1)/(2) * \ 1.67* 10^(-27) * 600,000^2 = 3.006 * 10^(-16) \ J\\\\K.E = (3.006 * 10^(-16) \ J \ \ eV)/(1.6 * 10^(-19) \ J) = 1878.75 \ eV`