Question

What is the value of x? Enter your answer in the box. Ft Triangle V T K with segment T Y such that Y is on segment V K, between V and K. Angle V T Y is congruent to angle Y T K. V T equals 77 feet, V Y equals 22 feet, V K equals x, and T K equals 87.5 feet.

Answer 1

47 ft

Explanation:

Answer 2

x=47 feet

Explanation:

Since angle VTY is congruent to angle VTK, segment TY bisects angle VTK. Since Y is on segment VK, between V and K, we can use the Angle Bisector Theorem, which states that:

`(VY)/(YK)=(VT)/(TK)`

`(22)/(YK)=(77)/(87.5)`

`YK=\frac{22{*}87.5}{77}`

`YK=25 feet`

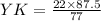
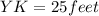
Now, X=VY+YK

Substituting the values, we get

X=
`22+25`

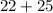
X=
`47 feet`