Question

Enter a recursive rule for the geometric sequence.

4, −16, 64, −256, ...



a1=

an=

Answer 1

a1= 4 an= -4a _n-1

Explanation:

just took the k12 test

Answer 2

`a_1=4`

`a_n=(-1)^(n-1)4^n`

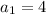
Explanation:

Given a G.P series i.e geometric sequence

4, −16, 64, −256, ...

We have to find the recursive rule for the geometric sequence.

We know that
`a_1` is the first term of the sequence.

Here
`a_1=4`

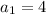
As, the nth term of Geometric progression is

`a_n=ar^(n-1)` where r is the common ratio

`\text{Common ratio=r=}(a_2)/(a_1)=(-16)/(4)=-4`

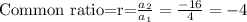
Hence the recursive formula is

`a_n=ar^(n-1)=4(-4)^(n-1)=(-1)^(n-1)4^n`