Question

Two people are standing on opposite sides of a hill. Person A makes an angle of elevation of 65° with the top of the hill and person B makes an angle of elevation of 80° with the top of the hill. The two people are standing 45 feet from each other. What is the distance from person B to the top of the hill? 29 ft 49 ft 71 ft 77 ft

Answer 1

Option 3. 71 ft. is the distance between B and top of the hill.

Explanation:

Let the height of the hill is h ft and the distance of A from the hill be x ft and distance from B to hill is y.

It is given distance between A and B is 45 ft. ∠BAO = 65° and ∠ABO = 80°.

We have to find the distance of B from the top of the hill.

Now from ΔACO
`tan 65 = (h)/(45-x) = 2.14`

`h=2.14(45-x)`

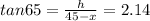
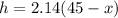
From ΔBCO
`tan80 = (h)/(x) = 5.67`

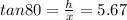
h = 5.67x

Now h = 5.67x = 2.14(45-x)

5.67x = 96.3 - 2.14x

2.14x + 5.67x = 96.3

7.81x = 96.3

x = 96.3/7.81 = 12.33 ft

Therefore
`cos80 = (x)/(OB)`

`0.174 = (12.33)/(OB)`

`OB = (12.33)/(.174)=70.86=71ft.`

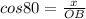
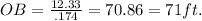
Therefore 71 ft is the distance between B and the top of the hill.