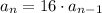Answer:
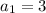
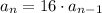
Explanation:
The explicit formula for the geometric sequence is given by:
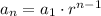 ....[1]
....[1]
where
 is the first term
is the first term
r is the common ratio of the consecutive terms
n is the number of terms
Given that:
The explicit rule for a sequence is given. by:
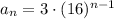
On comparing with equation [1] we have;
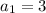 and r = 16
and r = 16
Use the recursive formula for the geometric sequence is:

Substitute the given values we have;
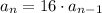
therefore, the recursive rule for the geometric sequence is,