What is the domain and range for the following function and its inverse?
f(x) = x2 – 2
f(x)
domain: x
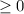
, range: y

f–1(x)
domain: x

, range: y
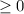
f(x)
domain: all real numbers, range: y

f–1(x)
domain: x

, range: all real numbers
f(x)
domain: all real numbers, range: all real numbers
f–1(x)
domain: all real numbers, range: all real numbers
f(x)
domain: x

, range: all real numbers
f–1(x)
domain: all real numbers, range: y=
