Question

Which is true regarding the system of equations? The system results in a false statement. The system results in an intersection at one point. The system results in parallel lines. The system results in a true statement because they are the same line.

Answer 1

the system true same line

Answer 2

The system results in a true statement because they are the same line.

Explanation:

The given system is

`\left \{ {{3x+y=23} \atop {6x +2y=46}} \right.`

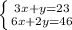
Notice that if you muliply the first equation by 2, you'll get the second equation

`\left \{ {{6x+2y=46} \atop {6x +2y=46}} \right.`

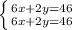
This means both equations represents the same line, or the lines are one on top of the other.

Therefore, this system has infinitetly many solutions, because they share all points.

So, the right answer is the last choice.