1.
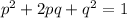 where in a population:
where in a population:
p - the frequency of the A allele
q - the frequency of the a allele
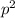 - the frequency of the AA homozygous genotype
- the frequency of the AA homozygous genotype
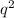 - the frequency of the aa homozygous genotype
- the frequency of the aa homozygous genotype
2pq - the frequency of the Aa heterozygous genotype
A population at equilibrium will have the sum of all the alleles at the locus equal to 1.
2. Conditions:
A. The breeding population must be large
B. No natural selection
C. The mating must occur randomly
D. No mutations to cause changes in allelic frequency.
E. No changes in allelic frequency due to immigration or emigration.
3. By comparing the actual genetic structure of a population with what we would expect from a Hardy-Weinberg equilibrium, we can determine how much it deviates from the baseline provided by the mathematical model. Depending on how large the deviation is, one or more of the model's assumptions are being violated. Thus, we can attempt to determine which one.