Answer:
The required value of x in the given logarithmic equation is -0.36
Explanation:
The given logarithmic equation is :
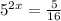
We need to find the required value of x in the given logarithmic equation.

Hence, the value of x in the given logarithmic equation is -0.36