Question

You want to rent a scooter. Sam’s Scooters charges a $30 fee plus $8 per hour. Rosie’s charges a $20 fee plus $10 per hour.

1. Create a system of equations that represents this situation.

2. Solve the system you created by substitution.

3. When does it make more sense to rent a scooter from Rosie’s? How do you know?

4. When does it make more sense to rent a scooter from Sam’s? How do you know?

5. Is there ever a time where it wouldn’t matter which store to choose? Explain.

6. If you were renting a scooter from both Rosie’s and Sam’s how much would you pay if you were planning on renting for 7 hours? Show your work.

Answer 1

1. C = 30+8h

C = 20 +10h

2.h = 5

C = 70

3. When Rosies cost less, we want to rent from Rosies

When h is less than 5 hours

4. When we want more then 5 hours ,we should rent from sams

5. At exactly 5 hours the costs are the same, so we can rent from either store.

6. Sams

C = 30+8(7) = 30 +56 = 86 dollars

Rosies

C = 20 +10(7) = 20+70 = 90 dollars

We want to rent from sams

Explanation:

Sams

C = 30+8h where h is the number of hours, C is the cost

Rosies

C = 20 +10h where h is the number of hours, C is the Cost

1. C = 30+8h

C = 20 +10h

Substitute the second equation into the first equation

20 +10 h = 30 +8 h

Subtract 8h from each side

20 +10 h -8h= 30 +8 h-8h

20 +2h = 30

Subtract 20 from each side

20-20 +2h = 30-20

2h = 10

Divide by 2

2h/2 =10/2

h = 5

Now find C

C = 20 +10h

C = 20 +10(5)

C = 20+50

C = 70

3. When Rosies cost less, we want to rent from Rosies

20 +10 h <= 30 +8 h

When h is less than 5 hours

They are equal at 5 hours

4. When we want more then 5 hours ,we should rent from sams

R <= S

5. At exactly 5 hours the costs are the same, so we can rent from either store.

6. Sams

C = 30+8(7) = 30 +56 = 86 dollars

Rosies

C = 20 +10(7) = 20+70 = 90 dollars

We want to rent from sams

Answer 2

Let the charges per hour for the scooter = x (hours) and the total rent of the scooter = y (dollars)

Part 1: We have,

Sam's scooter charges $30 fee plus $8 per hour.

Thus, the scooter charges are,
`y=30+8x`

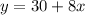
Rosie's scooter charges $20 fee plus $10 per hour.

Thus, the scooter charges are,
`y=20+10x`

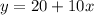
Thus, the system of equations is,
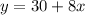`y=30+8x` and
`y=20+10x`

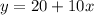
Part 2: On solving, we have,

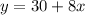`y=30+8x` ..............(1)

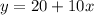`y=20+10x` ..............(2)

From (1), we will substitute the value of y in (2), we get,

`30+8x=20+10x` i.e.
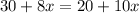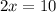`2x=10` i.e. x= 5.

So, (1) implies
`y=30+8* 5` i.e.
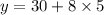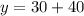`y=30+40` i.e. y= 70.

Thus, for 5 hours, the rent of the scooter is $70 for both.

Part 3: It is sensible to rent from Rosie's means that the rent charges of Rosie are low.

That is,
`30+8x>20+10x` i.e.
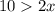`10>2x` i.e. x < 5.

So, whenever the number of hours are less than 5, it is sensible to rent the scooter at Rosie's.

Part 4: It is sensible to rent from Sam's means that the rent charges of Sam are low.

That is,
`30+8x<20+10x` i.e.
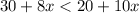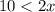`10<2x` i.e. x > 5.

So, whenever the number of hours are greater than 5, it is sensible to rent the scooter at Sam's.

Part 5: The time when it does not matter to choose a store will be when the prices of both the store are equal.

`30+8x=20+10x` i.e.
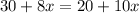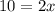`10=2x` i.e. x = 5.

Thus, for 5 hours, the rent of the scooter is $70 for both and it does not matter which store to choose.

Part 6: If we are planning to rent for 7 hours, we have x= 7.

So, the rent from Rosie's is,
`y=20+10* 7` i.e.
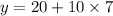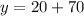`y=20+70` i.e. y= $90

So, the rent from Sam's is,
`y=30+8* 7` i.e.
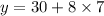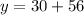`y=30+56` i.e. y= $86

So, the rent from Sam's and Rosie's for 7 hours are $86 and $90 respectively.