Answer:
1. x = 4
2. x = 20
Explanation:
1.
ΔABC and ΔAJK are similar (AA). Therefore the sides are in proportion:
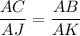
We have:
AC = 1 + 4 = 5
AJ = 1
AB = 1 + x
AK = 1
Substitute:
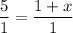
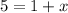 subtract 1 from both sides
subtract 1 from both sides
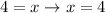
2.
ΔVUT and ΔVMN are similar (AA). Therefore the sides are in proportion:
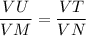
We hve:
VU = x + 8
VM = x
VT = 49
VN = 49 - 14 = 35
Substitute:
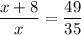 cross multiply
cross multiply
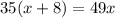 use the distributive property a(c + b) = ab + ac
use the distributive property a(c + b) = ab + ac
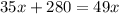 subtract 35x from both sides
subtract 35x from both sides
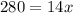 divide both sides by 14
divide both sides by 14
